Mais si le CIUN est bien un processus complexe, alors on peut explorer si et comment, les concepts issus des sciences de la complexité peuvent être utilisés pour analyser plus avant ce processus.

J’ai utilisé pour ce faire trois de ces concepts qui m’ont paru susceptibles de fournir de bons outils dans ce cas particulier : bifurcations et multistationnarité, dynamique des réseaux, et circuits de rétroaction positive. Il ne s’agit ni de tous les concepts disponibles, ni même de tous ceux qui auraient pu servir à l’analyse de l’exemple choisi. Je ne présenterai donc pas ici une analyse exhaustive de ce processus du point de vue de la complexité, mais trois exemples pour illustrer la faisabilité du projet et présenter les outils disponibles. J’appelle analyse dynamique les résultats de cette démarche, pour bien insister sur la différence d’avec l’analyse politique. Il ne s’agira donc pas pour moi, de « prendre parti [1] », mais d’offrir des outils pour la prise de parti.

Bifurcation et multistationnarité

1 - Présentation des concepts

Ce concept provient de la dynamique des systèmes non linéaires étudiée par la physique, essentiellement depuis les années 70. Il s’agit de systèmes complexes suffisamment simples pour être modélisés par des équations mathématiques appelées équations différentielles non linéaires, qui décrivent l’évolution de chaque variable du système en fonction du temps, sous l’influence des autres variables et de paramètres considérés comme constants. En général les systèmes dynamiques tendent vers un état dit stationnaire, ou singulier, (solution(s) du système d’équations différentielles) au cours duquel le comportement global se stabilise. Mais les systèmes non linéaires ont ceci de particulier qu’il y a plusieurs types d’états singuliers, et que la nature de l’état singulier atteint par un système dépend du système (nature des équations, valeur des paramètres), mais aussi de ce que l’on nomme les ‘conditions initiales’, c’est-à-dire l’état du système au temps zéro de l’expérience. Un état singulier, peut être un état stationnaire, où le système n’est pas au repos, mais où la valeur des variables n’évolue plus (comme la fameuse baignoire qui se vide à la même vitesse qu’elle s’emplit). Un autre état singulier peut être une oscillation, ou encore un chaos (dans lequel les variables ne prennent jamais deux fois la même valeur, ce qui donne des oscillations irrégulières comme celles d’un encéphalogramme) et enfin, le cas qui va nous intéresser le plus ici, la multistationnarité .

Dans ce cas, le système évolue vers l’un de deux (ou plusieurs) états stationnaires, en fonction de diverses caractéristiques, et notamment les conditions initiales. On appelle bassin d’attraction pour un des états l’ensemble des conditions initiales qui conduisent à cette solution. Souvent, il est possible de prévoir la nature des états stationnaires, mais pas de prédire lequel sera finalement ‘choisi’ par le système. Ainsi lors d’un match, on prévoit que l’une des équipes sera gagnante (ou qu’il y aura match nul), mais, en principe, on ne sait pas prédire laquelle.

Mais les choses se compliquent encore, car la nature même d’un état singulier peut dépendre des paramètres du système. Reprenons l’exemple du match de foot. Si l’une des équipes a un très bon gardien de but et l’autre non, l’issue du match est prédictible, il y a un seul état stationnaire. Mais que la deuxième équipe change de gardien de but, et l’issue devient incertaine, il y a multistationnarité. Le changement de ce seul joueur peut représenter le changement de paramètre qui va modifier la nature du jeu. On passe ainsi à un jeu sans issue prédictible, on dit qu’on a eu une bifurcation qui a fait passer le système d’un état stationnaire unique à deux états stationnaires possibles. On appelle ce type de bifurcation, une bifurcation fourche. En changeant 1 joueur (paramètre) sur 22, on a changé la nature du jeu, à condition que le paramètre en question ait été judicieusement choisi. En physique on parle de paramètre de contrôle , et on montre que, au voisinage d’une valeur critique, une toute petite variation de ce paramètre peut entraîner une bifurcation. Les dialecticiens reconnaîtront ici un des types de changement qualitatif à la Hegel [2]. Chaque fois qu’une petite modification d’un paramètre de contrôle modifie la nature de l’état singulier d’un système dynamique non linéaire, on parle de bifurcation. La bifurcation n’est dite fourche que si elle fait passer un système de un à deux (ou plus) états stationnaires possibles (ou inversement) [3].

Une illustration en est donnée dans la figure 1, où l’axe z (la profondeur) représente la variation du paramètre de contrôle.

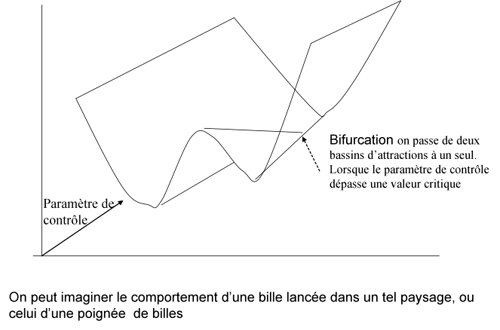
Les vallées représentent les bassins d’attractions. Il y en a deux avant la bifurcation, (plus un instable, sur la ligne de crête). Selon l’endroit d’où elle sera lancée, une bille aboutira au fond de l’une ou de l’autre vallée. Mais après la bifurcation il n’y a plus qu’un seul bassin d’attraction, d’où qu’elle soit lancée, la bille aboutira toujours au fond de la seule vallée existante.

2 - Application au cas de l’évolution du CIUN

Il va de soi qu’aucune modélisation sous forme d’équations différentielles n’est envisageable dans le cas qui nous préoccupe. L’utilisation du concept de bifurcation ne peut se faire que sous forme d‘une métaphore . Nous allons donc chercher si on peut trouver des comportements lors de l’évolution du CIUN qui rappellent les bifurcations, puis nous demander si une telle métaphore peut éclairer cette évolution, ou aider à poser de nouvelles questions. J’appellerai bifurcation une modification du comportement (et de la nature de l’état stationnaire) du système due à une petite modification des conditions [4].

J’ai exploré dans ce cadre, deux voies assez différentes.

D’une part, j’ai fait une liste de changements qui ont entraîné une modification de la dynamique du rassemblement. Telle est par exemple la décision que les partis signent en tant que tels l’appel du 11 Mai. En rigidifiant les rapports entre partis et collectif, elle a favorisé les rapports de force, qui ont abouti à l’émergence de deux camps que nous analyserons ci-dessous. (Lors des interviews, seules 3 personnes sur 17 ont dit avoir ressenti qu’il s’agissait d’une bifurcation). Un autre exemple, que personne n’a signalé, me paraît être l’appel à d’autres candidatures, lancé le 10 septembre lors d’une AG des collectifs. Examinons de plus près. On avait eu trois candidats potentiels (les 3 B [5]), de stature ou notoriété équivalente, et parfaitement incompatibles. Aucun ne se serait désisté pour un des deux autres, aucun compromis n’était possible. Avec le retrait de la LCR, la situation ne changeait pas radicalement. On avait un système à deux candidats incompatibles. Et on savait que chacun représentait un ‘bassin d’attraction’ constitué de membres différents des collectifs et de la gauche. Trois solutions pouvaient a priori être envisagées. Des primaires, une discussion permettant de trouver un consensus (voir ci-dessous), ou, solution retenue, un appel à de nouvelles candidatures qui se voulaient de consensus (un consensus ‘autoproclamé’ en quelque sorte, à ceci près qu’ils étaient deux et sont restés en lice jusqu’au bout [6]). Avec 4 candidatures la solution consistant à faire ‘choisir’ les collectifs locaux a paru évidente à tous, même s’il s’est avéré ultérieurement que les modalités de choix envisagées sous le terme commun de ‘double consensus’ étaient fort différentes. Autrement dit, la décision (dont il faut noter qu’elle a été prise sans discussion tant elle paraissait ‘évidente’) de faire un appel à nouvelles candidatures, s’est avérée lourde de conséquences, a changé la possible dynamique, a donc été une bifurcation, bien que, sur le moment (et même plus tard), personne n’en ait été conscient.

Il y a eu bien d’autres bifurcations dont la liste serait fastidieuse, mais qui toutes montrent que l’évolution du CIUN a dépendu de décisions qui n’étaient pas ‘fatales’, et dont certaines d’ailleurs ont été vécues comme bifurcation par quelques uns des participants. La plupart de ces bifurcations sont dues à des décision prises en dehors du CIUN (décision de la LCR, des socialistes antilibéraux, etc.). Dans certains cas on ne peut pas préciser le moment de la bifurcation. Par exemple, au départ, le PCF avait ‘proposé’ la candidature de sa secrétaire nationale. Les cause du blocage de ce parti sur cette candidature sont multiples (tensions internes, votes des collectifs en faveur de cette candidature, rétrécissement de l’union, agressivité de certains des partenaires ..) mais la plupart résultent en fait du fonctionnement (et des contradictions), soit des collectifs , soit du PCF lui-même [7]. D’ailleurs certains interviewés réfutaient l’idée d’une bifurcation car ils pensent qu’il s’agissait d’une position prise dès le début par le PCF.

L’intérêt d’un tel exercice est d’une part de mettre en évidence certains évènements qui ont pu paraître négligeables sur le moment à la plupart des participants, mais qui se sont avérés avoir eu un grand effet sur la dynamique. D’autre part, et plus largement il permet de déterminer les moments où l’évolution a pris une route particulière qui aurait pu être différente. La plupart du temps ces bifurcations proviennent de décisions politiques, et en conséquence ne sont pas fatales. L’intérêt en est donc rétrospectif en permettant de mieux comprendre ce qui s’est passé. Il s’agit d’un outil d’analyse qui permet de dépasser le « c’est la faute à … », pour étudier l’ensemble des moments où une autre décision aurait permis une autre dynamique (dont le résultat d‘ailleurs n’est pas non plus prédictible dans la mesure où d’autres bifurcations se seraient alors peut être présentées).

J’ai aussi utilisé la notion de bifurcation fourche d’une tout autre manière. Lorsqu’on a plusieurs candidats, on peut considérer qu’il y a là un système multistationnaire, où chaque candidat est une ‘solution’ possible du système, et où les bassins d’attraction peuvent être constitués des partisans de chaque candidat. Il faut alors déterminer la méthode de choix entre ces solutions. Le vote est la méthode la plus utilisée en général. Vote dans un corps électoral large (primaires proposées par J. Bové), ou vote dans les collectifs. Mais on n’a pas voulu parler de vote, on a parlé de ‘double consensus’ [8]. Une représentation du consensus peut elle être proposée d’un point de vue dynamique ? Puisqu’il s’agit d’une solution unique à laquelle tous se rallient, à partir de positions initialement divergentes, il y a bien eu une dynamique. Si on reprend la figure 1, on peut dire que les deux bassins d’attraction du premier plan représentent les partisans de deux candidats, et qu’une bifurcation fait passer le système de deux solutions à une seule. Cette métaphore suggère qu’il n’y a pas choix entre deux candidatures, il y a une modification du système qui fait qu’il n’y a plus qu’une seule candidature, qu’elle soit l’une des deux précédentes ou une autre. Quel est le paramètre de contrôle dont la modification peut faire passer le système de deux à un bassin d’attraction ? C’est évidemment un facteur humain, la volonté de consensus , dont la force doit dépasser un certain seuil pour que le consensus se réalise. Après l’AG du 9-10 décembre à St Ouen, qui a consacré l’impossibilité de trancher entre les candidatures en présence et conduit à la rupture, une tentative de la dernière chance a présenté toutes les caractéristiques de la recherche de consensus prise au sens de cette bifurcation. Il s’est agi de la candidature de Francis Wurtz qui a ‘presque’ réussi à faire consensus, mais la volonté n’en était pas assez forte et partagée, le ‘seuil’ de bifurcation n’a pas été atteint.

On voit que dans ce cas, l’utilisation du concept de bifurcation reste certes une métaphore, mais qui peut permettre de comprendre, voire (on peut rêver) de gérer les évènements au fur et à mesure. Un consensus ne peut pas être un vote, ne peut pas résulter du choix entre plusieurs candidats par quelque méthode de vote que ce soit. Un consensus résulte d’une discussion à l’issue de laquelle il n’y a qu’un seul candidat accepté par tous (Ce qui ne veut pas dire que, en l’absence constatée de consensus, le recours au vote n’était pas nécessaire, mais dans ce cas, il ne faut pas parler de consensus, mais de vote.). Et le ‘double consensus’ aurait nécessité une procédure impliquant obligatoirement un va et vient entre le CIUN et les collectifs jusqu’à dégager une candidature, que ce soit l’une de celles affichées ou une autre (comme celle de F. Wurtz ).

Réseaux et dynamique des réseaux

Depuis un certain nombre d’année le terme de ‘réseaux’ est (re)devenu à la mode, et s’applique même parfois à tort et à travers. Je vais m’appuyer ici sur ce que j’appelle ‘science des réseaux’, c’est-à-dire le corpus scientifique (récent) provenant essentiellement des mathématiques, de la physique, de l’informatique, des sciences de l’ingénieur, qui traite des propriétés générales des réseaux indépendamment de leur nature (physique ou sociale). Ce qui caractérise la « démarche réseau » est la volonté de prendre en compte, dans un système, à la fois les éléments et les interactions entre eux. Ceci n’est pas nouveau, c’est le cœur de la démarche dialectique, mais ce qui l’est, et qui change profondément les choses, c’est non seulement qu’on a pris conscience que les interactions ne sont généralement pas ‘linéaires’ (complexité), mais aussi qu’on travaille au niveau global de l’ensemble des interactions, et non des seules contradictions, prises chacune à son tour. Les réseaux sont donc des systèmes complexes, dont l’étude nécessite un point de vue particulier, et les études dont ils ont fait l’objet devraient pouvoir être utilisées dans le cadre de notre projet.

1 - Présentation des concepts

On appelle réseau un ensemble d’éléments en interaction. Ces interactions peuvent être statiques (un réseau de routes ou la carte du métro parisien), mais dans la plupart des réseaux elles sont dynamiques (un réseau d‘aéroports, un réseau d‘influences). Et d’entrée de jeu on voit qu’il y a une question de point de vue. On peut considérer un réseau routier comme statique (l’ensemble des villes et des routes qui les joignent), mais on peut aussi envisager le trafic sur ces routes ce qui introduit la dimension dynamique. De même le réseau des aéroports peut ne s’intéresser qu’aux vols ou aux compagnies, qui relient telle ville à telle autre, mais peut impliquer le trafic des aéroports, soit en terme de nombre d’avions, de nombre de passagers, voir de nombre de changements que ces passagers sont amenés à faire, etc. Un réseau d’amis peut représenter seulement les noms des personnes qui se fréquentent (réseau statique) ou impliquer aussi la nature des interactions, et leurs variations. Il en est de même d’un réseau militant. Pour chacune de ces questions, on va considérer un réseau différent, et utiliser des méthodes d’étude différentes. Il est donc important de réaliser dès l’abord que l’étude d’un réseau correspond à un point de vue, à une question que l’on se pose.

Il n’est pas question ici de résumer en quelques pages cette science des réseaux [9], mais de présenter quelques concepts qui m’ont servi d’outils pour comprendre certains aspects du fonctionnement du CIUN.

La première notion à dégager est celle de structure d’un réseau. Elle va être représentée par un graphe, dans lequel les éléments sont appelés les nœuds, reliés par les interactions (arcs ou connections), quelle que soit la nature de ces interactions. Le graphe est donc statique, et il existe un grand nombre de structures possibles de réseau, dont quelques uns sont représentés dans la figure 2.

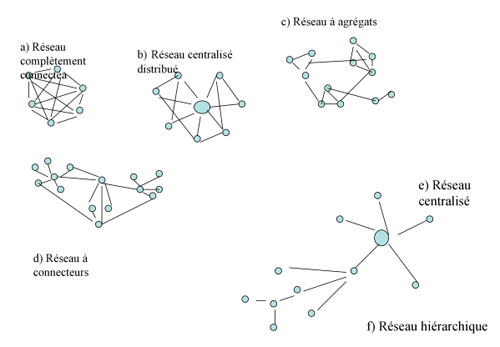
Les mathématiciens ont défini toutes sortes de grandeurs qui permettent de caractériser chacune de ces structures. On voit par exemple que ces graphes diffèrent pas le nombre moyen de connections nécessaires pour passer d’un élément à l’autre, pris chacun au hasard. On nomme ‘petit monde’ les réseaux où ce nombre est relativement faible par rapport au nombre total d’interactions. Par exemple, on a calculé qu’il ne faut jamais plus de 19 clics pour passer, sur le web, d’un site à un autre site pris au hasard, et ce alors qu’il y a des millions de sites.

Cette propriété n’est pas générale. Un réseau hiérarchique (f), ou un réseau constitué d’éléments placé sur un cercle et reliés simplement deux à deux (non représenté sur la figure) ne sont pas ‘petit monde’. Une autre propriété importante de ces structures est leur robustesse. Quel est l’effet de la rupture d’une connexion, de la disparition d’un élément ? On voit que, dans le réseau centralisé distribué (b), la disparition même du centre ne change pas la structure générale du réseau. Dans le réseau à connecteurs (d), la disparition d’un des nœuds à multiples connections peut avoir de fortes répercussions sur la structure du réseau, mais c’est dans le réseau centralisé (e) ou hiérarchique (f) que cette disparition détruit complètement le réseau.

On peut encore compléter le graphe par des flèches si les interactions ne sont pas réciproques, par des signes + et – qui indiquent que l’interaction est favorable ou défavorable à l’élément qui la reçoit, voire à des pondérations qui indiquent que les interactions sont plus ou moins ‘fortes’.

Par là, on se pose la question de la nature des interactions, on arrive donc à la notion de dynamique du réseau, de son fonctionnement. C’est à la fois ce qui est le plus intéressant mais le moins bien connu encore. Les questions sont foisonnantes, et n’ont pas toutes reçu de réponses satisfaisantes.

On peut se demander si le fonctionnement d’un réseau répond à la volonté d’un ou plusieurs membres du réseau, qui vont alors jouer le rôle de leader ou de chef d’orchestre, ou si au contraire il va émerger de l’ensemble du réseau (fonctionnement global, distribué, émergent ). Dans la nature, on connaît de nombreux cas de réseaux émergents, qu’il s’agisse du plus étudié d’entre eux, la colonie de fourmis, ou du plus évolué, le cerveau, qui n’a aucun centre décisionnel, mais qui constitue le réseau distribué émergent le plus efficace qui soit. Un autre réseau émergent est constitué par le web, que personne n’a construit ou imaginé, mais dont la structure et le fonctionnement résultent de … son fonctionnement.

Ce que l’on commence à bien savoir maintenant (du moins pour les réseaux simples, ou pour les réseaux simulés sur ordinateur), c’est que la dynamique d’un réseau est fortement dépendante de sa structure. Et réciproquement. En particulier, toutes les structures de réseau ne permettent pas un fonctionnement global émergent. Il s’agit là d’un domaine en pleine étude, mais les réseaux globaux émergents que je connais ont tous des structures petit monde. Les connections faciles entre tous les nœuds pourraient être une condition nécessaire à un tel fonctionnement.

Parler de dynamique c’est s’intéresser à la nature et au fonctionnement des connexions. On ne considérera ici que des réseaux où toutes les connexions sont de même nature. Or les études sur la dynamique des réseaux sont très compliquées. Dès que le réseau possède de nombreux nœuds, les scientifiques doivent avoir recours à des méthodes de simulation informatique, qui ne permettent pas toujours de comprendre ce qui se passe, mais simplement de prédire, ou d’expérimenter. Un très grand nombre de recherches actuelles concernent les langages informatiques qui permettent le mieux de réaliser ces simulations.

Certains travaux, en revanche concernent des réseaux qui, pour être complexes, n’en sont pas moins simples, c’est-à-dire constitués d’un nombre restreint de nœuds et de connections. Dans de tels cas, on peut recourir aux méthodes d’étude des systèmes dynamiques non linéaires et retrouver leurs comportements. Une méthode très prisée actuellement consiste à étudier ainsi des sous-réseaux, puis à les combiner, en cherchant si les propriétés se maintiennent lorsqu’on accroît progressivement la taille du réseau.

2 - Utilisation dans le cas de l’évolution du CIUN

La première notion utile dans ce cas est celle de graphe. Tracer le graphe d’un réseau réel, c’est se poser de nombreuses questions, c’est mettre en avant l’importance du point de vue, c’est donc se doter d’une méthode d’étude, non pas, pour le moment, dynamique, mais tout au moins globale.

On peut par exemple se poser la question des rapports entre le CIUN et les collectifs locaux (CLs ou CUALs). Le graphe qui les représente, figure 3, est un graphe quasi centré sur le CIUN, les seuls contacts entre CLs étant lors des trois assemblées générales, elles mêmes préparées par le CIUN. Peu de connections des CLs vers le CIUN. On peut comprendre que la disparition du CIUN a complètement ruiné le réseau, et on voit que ce réseau avait peu de chances de faire émerger quoi que ce soit qui n’ait pas été d’abord préparé par le CIUN.

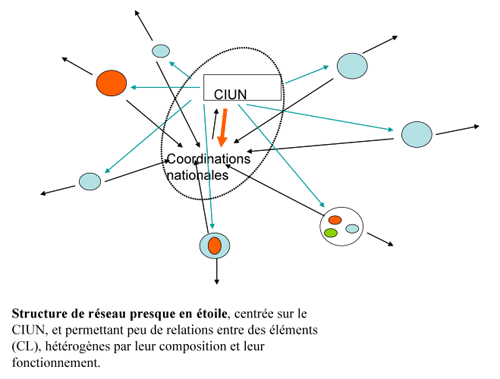
On pourrait aussi se demander quelle autre structure aurait été plus performante. Des propositions avaient été faites visant à faire venir des représentants des CLs au CIUN. De quelque façon qu’on imagine un tel système, il restait centré, et même hiérarchique, car il impliquait une organisation intermédiaire au niveau départemental, mais n’imaginait pas de méthodes d’interactions entre des CLs éloignés. Il n’était ni plus robuste, ni surtout plus émergent.

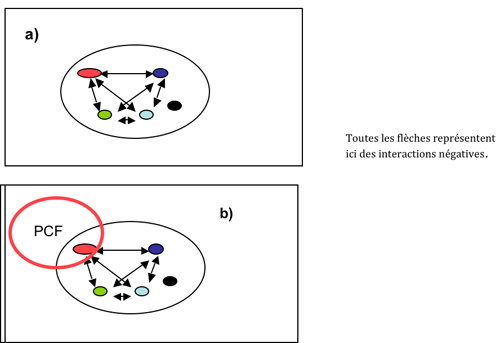
Cette technique du graphe peut aussi être utilisée pour étudier le CIUN lui-même. Cet exemple illustrera le fait que la représentation sous forme de graphe permet de se poser de multiples questions . La première question concerne les nœuds de ce graphe. Si on représente les 40 participants, le nombre de nœuds et de connections va devenir inextricable. Peut on regrouper les participants en éléments qui constitueront les nœuds ? Certes, mais ce regroupement va correspondre à des choix, donc aux questions que l’on se pose. On peut par exemple les regrouper selon la couleur des cheveux. Cela diminuerait le nombre de nœuds mais n’aurait à l’évidence aucun intérêt. Pendant la phase d’élaboration du texte ‘ambition et stratégie’, les regroupements pertinents se feront par rapport aux positions en présence, celle de la LCR, celle de PRS et celle du rédacteur du texte de compromis, Claude Debons. Ce regroupement, cessera d’être pertinent pendant la phase de ‘choix’ de la candidature. Cette fois, c’est en fonction du candidat qu’ils soutiennent que seront regroupés les membres du CIUN. 4 candidats, soient 5 groupes, le 5^e étant constitué de ceux qui ne voulaient pas choisir. Les connexions sont telles que chaque nœud entretient des relations négatives avec tous les autres nœuds (figure 4a).

Pour compléter on pourrait représenter le nombre des partisans de chaque candidat par la taille du nœud, mais je n’ai pas les données me permettant de le faire. Cependant, cette représentation ne tient pas compte d’un facteur important, la présence es qualité des représentants de partis, et en particulier du parti communiste. Ainsi les supporters de MGB ne sont peut être que 4 au sein de réseau, mais ils représentent la formation politique de loin la plus importante de cette coalition. Qui plus est, ils ne sont pas des membres comme les autres du CIUN, mais les représentants d’une formation dont ils se doivent de répercuter les positions. Comment représenter cette situation ? La figure 4b tente d’apporter une forme de réponse, en représentant l’intersection entre le CIUN et le PCF [10]. Cette figure attire l’attention sur la rigidité que cette formule introduit [11].

Ainsi représenté, cependant, le réseau est relativement simple, et on peut donc s’intéresser à sa dynamique. On voit qu’entre tous les nœuds se produisent des couples d’interactions négatives. Lorsque deux éléments sont reliés par deux interactions négatives (A refuse B qui refuse A), cela forme un circuit de rétroaction positive, ce qui est une condition nécessaire (en dynamique des systèmes non linéaires), de l’apparition d’une bistationnarité. Avant de pouvoir étudier la dynamique du réseau CIUN au cours de la recherche d’une candidature, il faut donc faire le détour par l’étude du rôle des circuits de rétroaction.

Circuits de rétroaction positive

1 - Présentation des concepts

Un circuit de rétroaction est un réseau dans lequel les interactions entre les éléments sont telles que, in fine, chaque élément exerce un effet sur lui-même. Si A influence B qui influence C qui influence A, alors, A va influencer A, de même que B influence B etc. Ces interactions peuvent être affectées d’un signe, on parle d’interaction négative si elle défavorise l’élément vers lequel elle est orientée, d’interaction positive si elle le favorise. Le circuit a également un signe : il est positif si l’influence in fine de chacun des éléments sur lui-même, est positive. Il est négatif dans le cas contraire On montre que, quel que soit le nombre d’éléments dans le circuit, son signe dépend uniquement de la parité des interactions directes négatives : un nombre impair d’interactions négatives entraîne un circuit de signe négatif, un nombre pair (y compris 0), correspond à un circuit de signe positif (on les désigne respectivement comme circuits de rétroaction négative ou positive [12].)

Les circuits de rétroaction négative sont bien connus, l’exemple type en est le thermostat : la température diminue le chauffage qui augmente la température, ce qui diminue le chauffage et ainsi de suite pour maintenir la température constante. A diminue B (interaction négative) qui augmente A (interaction positive). Il y a ici une seule interaction négative (nombre impair). C’est une homéostasie, l’augmentation d’un élément conduisant inéluctablement à sa diminution et réciproquement ... S’il existe des interactions non linéaires dans le circuit, le système, dans certaines conditions, peut présenter des oscillations. La présence d’un circuit négatif est la condition nécessaire (bien que non suffisante) à l’apparition d’oscillations dans un système non linéaire.

Des circuits de rétroaction dont l’importance est peut-être moins connue, sont les circuits de rétroaction positive qui vont nous concerner ici. On y voit souvent exclusivement l’emballement illimité qui caractérise par exemple l’explosion atomique. Mais la plupart du temps, les conditions dans lesquelles se réalise un circuit de rétroaction positive sont suffisamment contrôlées, pour ne laisser place à aucune catastrophe. Or il a été démontré [13] que la présence de circuits de rétroaction positive dans un système où certaines au moins des interactions sont non linéaires, est la condition nécessaire (et là encore non suffisante) à l’existence de multistationnarité. Parmi les circuits de rétroaction positive, celui qui nous intéresse ici est le circuit à double négation. Si A défavorise B, et B défavorise A, alors, une augmentation de A, en diminuant B, va contribuer à augmenter A et ainsi de suite, si bien qu’il ne restera au final plus que A. Le même raisonnement vaut pour B. Si le circuit de rétroaction est actif, le système devrait conduire à ce que l’un seulement des deux éléments subsiste (ou gagne). (On voit bien ici que le terme ‘positif’ ne connote aucun aspect ‘favorable’).

Dans la mesure où ceci se produit dans un réseau, il y a aussi la possibilité, si la ‘solution’ provoquée par la présence du circuit de rétraction positive est incompatible avec le reste du réseau, ou si aucune solution n’est possible, que celui-ci casse (C’est le cas lors d’un match de foot, si les supporters d’un camp envahissent le stade !!).

2 - Utilisation dans le cas de l’évolution du CIUN considéré comme un réseau

Nous avons laissé le graphe du CIUN au niveau de la figure 4b. où chaque groupe de participants de ce collectif était en interaction négative avec les autres, ce qui représentait autant de couples de rétroactions négatives, donc autant de circuits de rétroaction positive, donc autant de bassins d’attractions que de candidats. À l’évidence, une situation assez inextricable, qui aurait pu conduire à une discussion pour aboutir, soit à un consensus, soit à la décision que celui-ci était impossible, et qu’il fallait changer de stratégie. Mais ce n’est pas ce qui s‘est passé. Le PCF a insisté pour que le CIUN, en tant qu’organe informel et non représentatif de coordination des collectifs locaux, ne soit pas le lieu de cette prise de décision, mais que ce soient d’abord les collectifs qui choisissent. La discussion n’a donc pas eu lieu, du moins pas au début, au sein du CIUN qui s’est contenté de discuter (d’ailleurs sans pouvoir se mettre d’accord), sur les consignes à envoyer aux collectifs.

Or cette absence de discussion a exacerbé des tensions implicites, qui ont conduit à l’émergence d’une tout autre dynamique représentée sur la figure 5. L’ensemble des participants sauf les représentants es qualité du PCF, se sont regroupés progressivement, en un ‘camp’ implicite, en dépit de leurs divergences, unis seulement sur le refus de la candidature de MGB. De leur côté, les représentants du PCF ont, dans un premier temps simplement refusé ce refus (pas de préalable).

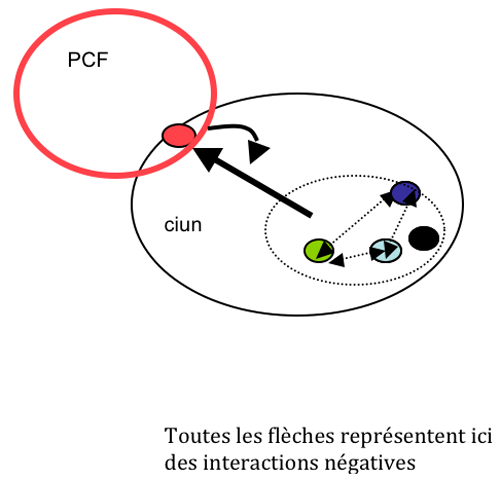
Mais on voit que cela forme maintenant un circuit unique de rétroaction positive par double négation. Avec trois solutions, la victoire de l’un des deux ‘camps ‘ (et l’hétérogénéité du camp ‘anti-MGB’ ne permet pas de présager de ce que son éventuelle victoire aurait donné), ou la rupture du réseau. Il s’en est suivi un ‘bras de fer, qui a préparé la rupture consommée lors de l’AG des collectifs (il y a là une dynamique différente dont l’étude nécessiterait de travailler sur les Procès Verbaux de ces collectifs).

Seuls deux des interviewés avaient clairement perçu cette modification progressive de la dynamique au sein du CIUN où l’on peut voir l’émergence d’une sorte d’auto-organisation en deux ‘camps’, que personne n’avait voulue au départ. La méthode d’étude illustrée ici permet donc de mettre en évidence des évolutions importantes, et leurs causes dynamiques. Il est clair cependant qu’elle ne met pas, qu’elle ne peut pas mettre en évidence les causes politiques de ces évolutions. Par exemple, l’interaction négative venant du PCF, est dynamiquement la même qu’il s’agisse de refuser le refus des autres (pas de préalable), ou de refuser toute autre candidature (MGB seule candidate possible). Politiquement, bien sur, c’est différent.

3 - Pourquoi certaines actions ont-elles l’effet inverse de celui prévu ?

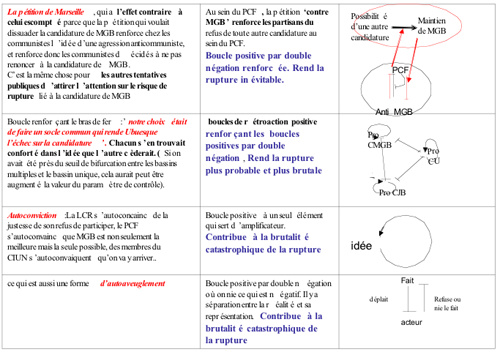
La recherche des circuits de rétroaction positive à l’œuvre lors de l’évolution du CIUN m’a aussi permis de voir le rôle de ces circuits dans des cas où l’action s’est retournée contre le but que ses protagonistes s’étaient fixés. La figure 6 regroupe ces cas, j’en détaillerai ici un seul, le premier. Vers la fin du mois de novembre 2007, alors que les tensions commençaient à être fortes au sein du CIUN, mais que le travail était relativement serein et très sérieux dans les collectifs locaux qui travaillaient sur le choix de la candidature, un évènement a fortement précipité la rupture. Une pétition, issue de militants des Bouches du Rhône, prenant prétexte du retrait de José Bové [14], demandait notamment à MGB de retirer sa candidature. Cette pétition n’aurait peut-être pas eue une forte incidence si une majorité de membres du CIUN ne l’avaient signée. Ce faisant, ils avaient voulu avertir le PCF, puisqu’il n’était pas possible d’en discuter au sein du CIUN, des risques énormes de rupture au cas où la candidature de MGB serait maintenue. Ils (tout au moins ceux qui m’en ont parlé, et avaient d’ailleurs reconnu que c’était une erreur), en escomptaient que le PCF prendrait ainsi conscience de la détermination de ceux qui refusaient que sa secrétaire nationale soit la candidate d’union. Ils espéraient ainsi éviter la rupture qu’ils prévoyaient déjà.

Mais c’était sans compter avec les circuits de rétroaction positive ! En signant cette pétition, ils voulaient donner un signal au PCF pour affaiblir sa position négative par rapport aux autres candidatures. Mais ce signal a été ressenti par la grande majorité des militants communistes, impliqués ou non dans les collectifs, comme une manifestation violente d’anticommunisme. Ce signal négatif a donc défavorisé ceux de la direction du PCF qui étaient pour la démarche unitaire, (boucle positive par double négation) et a donc, in fine, renforcé la détermination de ce parti à maintenir la candidature de sa secrétaire nationale.

La figure 6 montre 3 autres boucles de rétroaction positive à l’origine d’une situation inverse de celle voulue par les acteurs. On se rappelle ici ‘Alice à travers le miroir’ qui doit tourner le dos à son objectif pour l’atteindre. Il s’agit peut être de la manifestation la plus spectaculaire du caractère complexe d’un processus. On peut m’objecter qu’on n’a pas besoin des circuits de rétroaction pour la comprendre. J’avancerais que la formalisation que peut représenter cette méthode, oblige à voir ce qu’il est éventuellement possible de voir sans elle.

Ces outils peuvent ils être utilisés pour l’action ?

Les quelques exemples ci-dessus montrent comment l’utilisation des concepts issus des sciences de la complexité peut préciser une démarche de type dialectique (étude de la dynamique et des interactions en jeu lors d’un processus), et amener à mieux cerner rétroactivement le déroulement d’un processus. Encore une fois, cette analyse dynamique ne remplace pas l’analyse politique . Elle ne dit pas ce qui aurait dû être fait pour obtenir tel ou tel résultat. Elle démêle seulement des interactions plus compliquées et plus nombreuses que celles qui sont généralement énoncées lorsqu’on omet ces méthodes. Ainsi, un grand nombre d’analyses politiques sur cette période sont unilatérales, mettant l‘accent sur une cause, ou sur une famille de causes. Même lorsqu’elles prennent en compte plusieurs causes, elles n’en cherchent pas les rétroactions, et se contentent le plus souvent d’en faire la liste. L’analyse dynamique peut donc être proposée comme outil pour comprendre l’évolution d’un processus passé. Elle aurait tout avantage à être pratiquée par tous ceux qui tirent les leçons du passé pour préparer politiquement l’avenir. En effet, autant il est important de tirer ces leçons, autant il est nécessaire de ne pas se tromper, de ne pas se contenter d’une analyse unilatérale ou simpliste, voire déterministe-fataliste : « si ça a raté, c’est que ça ne pouvait pas réussir, donc cette porte est définitivement fermée, ce chemin est clairement une impasse ! » Non ! Si ça a raté, c’est que le déroulement, les décisions, les évènements ont conduit à l’émergence de l’échec. A plusieurs moments des décisions différentes auraient pu être prises, avec des résultats peut-être différents [15]. À quel moment cet échec était il devenu inévitable ? Personne n’est d‘accord là-dessus, ce qui illustre l’absence de fatalité de l’issue.

Dans ce contexte, l’analyse dynamique aide à déterminer les moments de bifurcation, les boucles de rétroaction conduisant à des impasses. Elle aide l’analyse politique à tirer du passé des leçons plus exactes, et plus nuancées. Les conclusions tirées du passé ne pourront cependant être que politiques, car elles résultent de choix, alors que l’analyse dynamique insiste sur les possibles . L’analyse dynamique permettra par exemple à ceux qui ne souhaitent pas, politiquement, abandonner la voie du rassemblement antilibéral, de faire la liste la plus complète possible des obstacles, et de jauger s’il est possible de mieux les surmonter.

Mais on voit là poindre une autre question, autrement redoutable. L’analyse dynamique pourrait-elle aider l’action, par exemple en aidant, en temps réel à la prise de décisions ? Cette question même est elle compatible avec l’absence de prédictibilité des processus complexes ? Or s’il n’y avait aucune prise sur la dynamique d’un processus, la militance ne servirait à rien ! Je n’apporterai ci qu’une réponse partielle. Dans le cas où les résultats de la dynamique sont prévisibles mais non prédictibles, le rôle des militants est de favoriser le résultat qu’ils ambitionnent (on appelle cela en physique la brisure de symétrie lors d’une bifurcation fourche).

Ainsi dans le cas du CIUN, une analyse dynamique ‘prospective’ aurait-elle pu contribuer à une autre dynamique, faire réussir le processus, aider à éviter des erreurs, à empêcher à tout le moins une rupture brutale ? J’ai interrogé sur ce point ceux d’entre ses membres qui ont assisté aux comptes rendus que j’ai faits de mon travail, mais les réponses ont été au mieux, mitigées.

Une chose est certaine, l’analyse dynamique est impossible dans des conditions d’ambiguïté, de non-dits, de rapports de force qui ont prévalu vers la fin du CIUN. En ce sens, elle représente aussi une ‘démarche’ , susceptible d’influer sur le déroulement d‘un processus parce qu’elle conduit les participants à adopter une attitude réflexive, méthodologique, dynamique, dialectique et globale...et à tenter de la faire partager. Pour le reste, la discussion reste ouverte, et il y faudra sûrement de multiples expériences.

Lien vers la première partie : des processus complexes

Lien vers la troisième partie : méthodes d’étude des systèmes complexes utilisables pour l’action : l’exemple des réseaux militants ?